Эквивалентный диаметр воздуховода: формула, расчет, фишки и секреты
Аэродинамическое сопротивление круглого воздуховода можно посчитать в одну формулу. Причем чем выше скорость, тем выше сопротивление. А как быть с прямоугольными воздуховодами? Там действуют совсем другие принципы...
Содержание статьи:
Действительно, как сравнить, в каком воздуховоде будут больше потери на трение: 700х300 или 500х400?
Давайте представим, как будет рассуждать инженер, столкнувшись с такой задачей. Скорее всего он решит действовать через площадь воздуховода и скорость воздуха в нем:
- Площадь сечения первого (700*300=210 000мм²) больше, чем второго (500*400=200 000мм²), значит скорость воздуха ниже в первом воздуховоде и, следовательно, должно быть ниже и сопротивление.
Но эта логика ошибочна и в данном случае ведёт к неверному результату. Чтобы сделать правильный расчет (см. в конце статьи), прежде всего нужно обратиться к понятию "эквивалетного диаметра воздуховода".
|
Эквивалентный диаметр прямоугольного воздуховода — это диаметр воображаемого круглого воздуховода, в котором потеря давления на трение была бы равна потере давления на трение в исходном прямоугольном воздуховоде при одинаковой длине обоих воздуховодов. |
В книгах и учебниках В. Н. Богословского такой диаметр называется «Эквивалентный по скорости диаметр», в литературе П. Н. Каменева — «Равновеликий диаметр по потерям на трение».
Калькулятор для расчета эквивалентного диаметра онлайн
Для удобства наших читателей мы подготовили онлайн калькулятор, который помогает не только определить эквивалентный диаметр для того или иного воздуховода, но и подобрать сечение воздуховода, если диаметр уже известен.
Хочу такой же калькулятор себе на сайт
Калькулятор 1
Расчет эквивалентного диаметра
мм
мм
Эквивалентный диаметр:
Калькулятор 2
Расчет второй стороны, если известна первая
мм
мм
Сторона B:
Калькулятор 3
Выбор воздуховода по диаметру
мм
Хочу такой же калькулятор себе на сайт Ссылка на этот расчет:
В программе представлено сразу три калькулятора:
- Первый рассчитывает эквивалентный диаметр исходя из ширины и высоты (А и В) воздуховода.
- Второй помогает найти точное значение второго измерения (ширины или высоты), если известен экв. диаметр и первое измерение.
- Третий калькулятор подбирает все возможные допустимые сечения воздуховодов для заданного эквивалентного диаметра. Сечения кратны 50 мм, а соотношение сторон не более 3 к 1.
Если вам нужно проверить конкретное сечение (не кратное 50 мм или с соотношением сторон более чем 3 к 1, то воспользуйтесь вторым калькулятором.
Формула эквивалентного диаметра воздуховодов
Эквивалентный диаметр прямоугольного воздуховода вычисляется по формуле:
- Dэкв_пр = 2·А·В / (А+В), где А и В — ширина и высота прямоугольного воздуховода.
Например, в результате расчета вентиляции получился воздуходод 500х300. Ему соответствует эквивалентный диаметр 2·500·300 / (500+300) = 375 мм. Это означает, что круглый воздуховод диаметром 375 мм будет иметь такое же аэродинамическое сопротивление, что и прямоугольный воздуховод 500×300 мм.
Эквивалентный диаметр квадратного воздуховода равен стороне квадрата:
- Dэкв_кв = 2·А·А / (А+А) = А.
И этот факт весьма интересен, ведь обычно чем больше площадь сечения воздуховода, тем ниже его сопротивление. Однако круглая форма сечения воздуховода имеет наилучшие аэродинамические показатели. Именно поэтому сопротивление квадратного и круглого воздуховодов равны, хотя площадь сечния квадратного воздуховода на 27% больше площади сечения круглого воздуховода.
В общем случае формула для эквивалентного диаметра воздуховода выглядит следующим образом:
- Dэкв = 4·S / П, где S и П — соответственно, площадь и периметр воздуховода.
Используя эту формулу можно подтвердить правильность вышеприведённых формул для прямоугольного и квадратного воздуховодов, а также убедиться в том, что эквивалентный диаметр круглого воздуховода равен диаметру этого воздуховода:
- Dкругл = 4·π·R2 / 2·π·R = 2R = D.
Таблица эквивалентных диаметров
Для расчета может помочь таблица эквивалентного диаметра воздуховодов
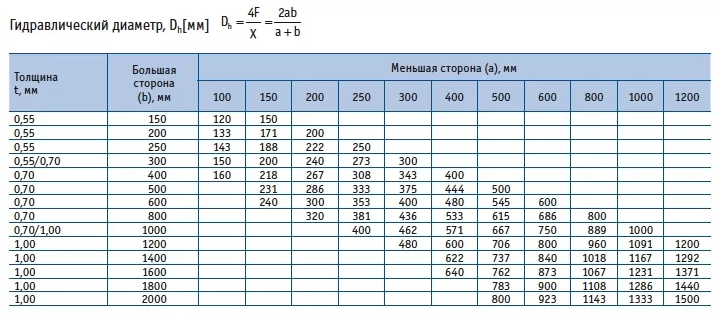
Пример расчета эквивалентного диаметра воздуховодов
В качестве примера определим эквивалентный диаметр воздуховода 600×300:
Dэкв_600_300 = 2·600·300 / (600+300) = 400 мм.
Фишки и секреты
Эквивалетный диаметр и металлоёмкость
Интересно отметить, что площадь сечения круглого воздуховодам диаметром 400 мм составляет 0,126 м2, а площадь сечения воздуховода 600×300 составляет 0,18 м2, что на 42% больше. Расход стали на 1 метр круглого воздуховода сечением 400 мм составляет 1,25 м2, а на 1 метр воздуховода сечением 600×300 — 1,8 м2, что на 44% больше.
Таким образом, любой аналогичный круглому прямоугольный воздуховод значительно проигрывает ему как в компактности, так и в металлоемкости.
Рассмотрим ещё один пример — определим эквивалентный диаметр воздуховода 500×100 мм:
Dэкв_500_100 = 2·500·100 / (500+100) = 167 мм.
Здесь разница в площади сечения и в металлоемкости достигает 2,5 раз. Таким образом, формула эквивалентного диаметра для прямоугольного воздуховода объясняет тот факт, что чем больше «расплющен» воздуховод (чем больше разница между значениями А и В), тем менее эффективен этот воздуховод с аэродинамической точки зрения.
Это одна из причин, по которой в вентиляционной технике не рекомендуется применять воздуховоды, в сечении которых одна сторона превышает другую более чем в три раза.
Диаметр квадратного воздуховода
Интересно отметить, что площадь сечения квадратного воздуховода всегда на 27% больше, чем вписанного в него круглого воздуховода. Однако их эквивалетные диаметры равны:
- Dэкв_кругл = D
- Dэкв_квадр = 2*A*A/(A+A) = A = D.

Итак, при прочих равных выгоднее использовать круглый воздуховод, чем квадратный, даже не смотря на то, что площадь сечения у него выше, а скорость будет ниже. Сопротивление будет в точности равно круглому воздуховоду!
Эквивалетный диаметр воздуховода с соотношением сторон 3:1
В вентиляции НЕ принято применять прямоугольные воздуховоды с соотношением сторон более, чем 3 к 1. То есть 900х300 - это допустимый вариант, а 900х200 или 800х200 - плохой и очень нежелательный.
Давайте определим, чему равен эквивалетный диаметр прямоугольного воздуховода с соотношением сторон 3 к 1:
- Dэкв = 2*A*(A/3) / (A + A/3) = (2A/3) / (4A/3) = A/2.
Оказывается, экв. диаметр такого воздуховода равен половине его длинной стороны.
Просто фантастика: один расплющенный воздуховод или много квадратных?
Продолжим расчет из предыдущего пункта. Что лучше - воздуховод с соотношением сторон 3 к 1 (Dэкв = A/2) или три квадратных воздуховода со стороной А/3?
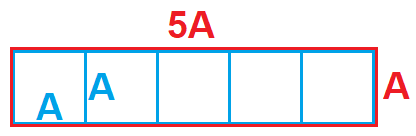
Красный плоский воздуховод со сторонами 5АхА можно разделить на 5 квадратных воздуховодов АхА. Выгодно ли это делать?
Другими словами, что если 900х300 заменить на три 300х300 - что выгоднее?
- Dэкв_900_300 = 2*900*300 / (900+300) = 450 мм.
- Dэкв_300_300 = 300 мм.
Площади сечений по эквивалетным диаметрам:
- S_450 = pi*450²/4 = 0,16 м²
- S_300 = 3* pi*300²/4 = 0,212 м²
С точки зрения эквивалетных диаметров оказывается, что три воздуховода 300х300 аж на ТРЕТЬ (32,5%) выгоднее, чем 900х300.
Теперь посчитаем аэродинамическое сопротивление. Для примера возьмем общий расход воздуха 3600 м³/ч для 900х300. Тогда на каждый воздуховод 300х300 выпадет 3600/3 = 1200 м³/ч:
- для расхода 3600 м³/ч: p_900_300 = 0,881 Па/м
- для расхода 1200 м³/ч: p_300_300 = 0,846 Па/м
Вот это удивительно! Оказывается, любой слишком плоский воздуховод выгоднее разделить на несколько квадратных или даже круглых! В данном случае мы получили выгоду 4%.

В микроканальных теплообменниках так и делается: один плоский канал разбивается на несколько круглых. Выгода как в плане сопротивления, так и в плане теплообмена.
Если бы соотношение сторон было 10 к 1, то разница будет аж в 3,5 раза:
- По итогам расчета вентиляции расход составил 5000 м³/ч, воздуховод 2000х200, сопротивление 4,362 Па/м
- Расход 500 м³/ч, 10 параллельных воздуховодов 200х200, сопротивление 1,22 Па/м
- Сопротивление во втором случае меньше в 3,57 раза!
И другой пример:
- Расход 20 000 м³/ч, воздуховод 4000х400, сопротивление 1,927 Па/м
- Расход 2 000 м³/ч, 10 параллельных воздуховодов 400х400, сопротивление 0,532 Па/м
- Сопротивление во втором случае меньше в 3,62 раза!
И ещё один пример: 500х100 или 5 штук 100х100:
- На объекте площадью 100 м² с высотой потолков 3,5 метра требуется обеспечить кратность 2. Расход составляет 100*3,5*2 = 700 м³/ч, воздуховод был подобран 500х100, сопротивление 5,391 Па/м
- Расход 140 м³/ч, 5 параллельных воздуховодов 100х100, сопротивление 3,533 Па/м
- И даже на малых диаметрах второй вариант выгоднее - более чем в 1,5 раза!
Единственная тонкость: расчет НЕ учитывает сопротивление коллектора на этапе разъединения большого воздуховода на 3 мелких и их последующего соединения. Если такие коллекторы нужны, то они "съедят" часть выгоды.
Как быстро подобрать воздуховоды, зная эквивалетный диаметр
Допустим, при расчете сечения воздуховодов оказалось, что эквивалентный диаметр равен 320 мм. Как понять, какие воздуховоды вообще стоит рассматривать? Конечно, мы рекомендуем пользоваться нашими онлайн калькуляторами, но что если их нет под рукой?
Тогда рассуждения должны быть следующими:
- Эквивалетному диаметру 320 мм соответствует круглый воздуховод 320 мм. Ближайший больший из стандартного ряда - 400мм. Но ближайший меньший - 315 мм - не сильно меньше. Скорее всего он тоже подойдет.
- Эквивалетному диаметру 320 мм соответствует прямоугольный воздуховод 320х320. Значит, точно подойдет 350х350, и скорее всего 300х350
- Максимальная разумная ширина прямоугольного воздуховода (чтобы соотношение сторон было не более, чем 3 к 1) составит 2 экв.диаметра (640 мм для нашего примера). Почему это так? Смотрите следующий пункт.
Как быстро подобрать самый низкий воздуховод, зная эквивалетный диаметр
Ещё одна интересная фишка. Например, эквивалентный диаметр равен 300 мм. Как найти самый низкий из всех возможных воздуховодов, но чтобы соотношение сторон укладывалось в рекомендации (т.е. было не более 3 к 1)?
Ранее мы считали эквивалетный диаметр воздуховода со сторонами в соотношении 3 к 1 (А и А/3):
- Dэкв = 2*A*(A/3) / (A + A/3) = (2A/3) / (4A/3) = A/2.
Оказывается, экв. диаметр равен половине длинной стороны! Значит, чтобы найти длинную сторону самого расплющенного воздуховода, нужно экв. диаметр умножить на 2 (А = 2*Dэкв).
Итак, если Dэкв=300, то A = 600, а вторая сторона B = А/3 = 200. Самый плоский воздуховод получится 600х200.
Аналогично для Dэкв=450 получим: А = 900, B = A/3 = 300. Самый плоский воздуховод будет 900х300.
И ещё один пример: Dэкв=240. Тогда А = 480, B = A/3 = 160. Можно принять 500х150, а лучше 400х200.
Решение задачи, о которой говорили в начале статьи
В самом начале статьи мы пытались выяснить, у какого воздуховода, 700х300 или 500х400, будет меньше сопротивление для одного и того же расхода воздуха. Причем так как площадь первого больше, то мы уже знаем, что скорость воздуха в нем будет меньше.
Давайте посчитаем эквивалентные диаметры:
- De1 = 2*700*300 / (700+300) = 420мм
- De2 = 2*500*400 / (500+400) = 444мм
Вот удивительное дело: сечение первого воздуховода БОЛЬШЕ по площади, но МЕНЬШЕ по эквивалентному диаметру. При расчете аэродинамического сопротивления решающее значение будем иметь именно эквивалентный диаметр. Раз он меньше, то сопротивление будет больше.
Итак, сопротивление воздуховода 700х300 БОЛЬШЕ, чем 500х400 для одного и того же расхода воздуха. При прочих равных выгоднее использовать именно 500х400.
|
Общее правило гласит: при прочих равных нужно выбирать более квадратный воздуховод (менее расплющенный, т.е. с меньшим соотношением сторон) |
Действительно, соотношение сторон воздуховода 700х300 составляет 700/300=2,3. Соотношение сторон второго воздуховода составляет 500/400=1,25. Это меньше, чем 2,3, поэтому выгоднее использовать воздуховод 500х400.
Дополнительные материалы
Комментарии читателей

Виктор
Шикарная подача информации, спасибо!
Оставить комментарий